Back to publications

TRANSIENT RESPONSE OF ROTOR MODEL

1. BACKGROUNDS
2. EXAMPLES OF CALCULATIONS AND OUTPUTS – LINEAR SPRING SUPPORTS
2.2 EXAMPLES OF CALCULATIONS AND OUTPUTS – DAMPER SUPPORTS

1. backgrounds

Squeeze-film damper model

Fig.1 Squeeze-film damper model
1 – vibrator;
2 – case;
3 – clearance with oil

Nomenclature:
δ-clearance, m;
e – orbit radius;
ε=e/δ - eccentricity;
ω- angle rotation speed;
Ω- whirl speed;
R- damper radius, m;
L - damper length, m;
μ– dynamical viscosity,
Ns/m2;
K – stiffness coefficient;
C – damping coefficient

Table 1
Approximate models of the damper performances (laminar flow, = const)

Approximate models of the damper performances

 

Pressure distribution in squeeze-film damper

Fig. 2. Pressure distribution in squeeze-film damper
δ=0.228 mm; l = 12.7 mm; D=104.3 mm; μ=0.0217; n = 1000 rpm; ε=0.4
Reynolds boundary conditions

Damping characteristics of squeeze-film damper

Fig. 3. Damping characteristics of squeeze-film damper
δ=0.228 mm; l = 12.7 mm; D=104.3 mm;μ =0.0217; n = 1000 rpm; ε=0.4;
Red line – Reynolds boundary conditions

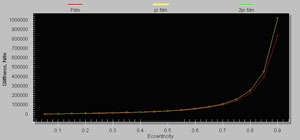
Stiffness characteristics of squeeze-film damper

Fig. 4. Stiffness characteristics of squeeze-film damper
δ=0.228 mm; l = 12.7 mm; D=104.3 mm; μ=0.0217; n = 1000 rpm supports; ε=0.4;
Red line – Reynolds boundary conditions

Table 2 HYDRODYNAMIC FORCES (LAMINAR FLOW)

HYDRODYNAMIC FORCES