Damper Supports, 4.2 Design of a HDFE, Alfa-Tranzit Co.

4.2 Design of a HDFE

HDFE design can be separated into two stages: HD design and Flexible element design. Below are given two examples of such design.

EXAMPLE 1

Design of a HD with a "squirrel-cage" type flexible element.

Input data

· Total support stiffness E = 0.4o10⁸ N/m;

· Damping N > 10000 Ns/m;

· Operating speed n = 14000 rpm = 1465 s^-1 ;

· Oil viscosity m = 0.266o10^-2 Ns/m²;

· Lumped bearing mass m_B= 33.43 kg;

· The damper diameter D = 130 mm.

1. Defermination of an optimal damper clearance d by recommended gravity parameter.

Considering W_B =m_Bg it is possible to assume a value =0.1 and

= (33.43 o 9.81)/(33.43 o 1465² o 0.1)

0.000045 i = 0.045 mm

To match manufacturing requirements we assume d=0.1mm.

2. The parameter B=0.1 value determines the damper length L_R:

L_R = =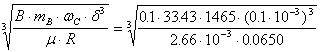

= 0.0305 i = 30.5 mm

3. Calculation of the damper dynamic performances.

The damper dynamic performances (stiffness and damping) are calculated after the main dimensions are determined as to fit the requirements.

The approximate calculations use both "p-film" and "2p-film models. The centered HD is to have lower stiffness than the “squirrel-cage”

The calculations below are related to a sealed by its ends ("long" damper) with a few oil supplying holes, Fig.11b. For the e=0.4 eccentricity the two film models give the following result:

“2p-film”.

C = =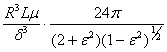

= =

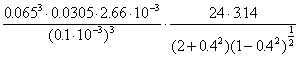= 848250 Ns/m

E = 0

“p-film”.

N = =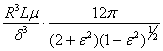

= =

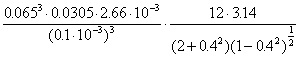= 424126 Ns/m

E = =

= 0.173o10⁹ N/m

The stiffness and damping exceed the needed values so much, that it is nesessary to consider another type of the damper.

4. Two versions are considered below

· a sealed damper with a central oil supply groove, Fig.11e;

· a not sealed damper with a few oil supplying holes, Fig 11a.

Both versions suit to a "short" damper model with reduced

length L_R = 30.5 mm

Two film models are analysed at e=0.4 eccentricity

“2p-film”.

C = =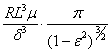

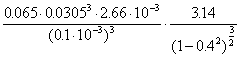= = 20010 Ns/m

E = 0

p-film”.

N = 10005 Ns/m

E = =

= 0.815 o 10⁷ N/m

For damper with the holes

L = L_R =30.5 mm.

For damper with the central annular groove

L₁=L₂ =15.25 mm

NOTE: The approximate solutions used here do not consider oil supply pressure, so the cavitating region length is not determined. The design is performed in such a manner as to meet needed performances at any cavitation state.

4. The next step is ajustment of the damper performances to the rotor dynamic system. This procedure uses stiffness parameters obtained out of rotor dynamics analysis. Here will be obtained new performances of the dynamic system including the determined damper: suports loads, displacements, vibration velocities.

It is necessary to note that the ajustment procedure can cause a larger eccentricity value and the dynamic transmissibility can become nearer to value 1. If so, the damper length can be reduced or the clearance can be increased under the B parameter control.

5. Actual performances of the damper and rotor system can be

obtained by testing of a special rig or by engine test.

6. Retain stiffness of the Flexible element

E _a = E_S - E = 0.4 o 10⁸ - 0.0815o10⁸ = 0.3185o10⁸ N/m

EXAMPLE 2

Stiffness and stress analysis of a "squirrel - cage" type flexible element.

Initial Data:

· Weigt of rotor lumped at either of the bearing station G = 1700 N;

· Maximal radial displacement d = 0.275 mm;

· The axial slots length and width - l = 75 mm; A? = 5 mm;

· Flexible cylinder outer and inner diameters D_o=280 mm, D_i=271mm;

· Number of flexible bars n = 96;

· The cylinder material 18X2H4MA (Russian standard), Young module E=0.19*10e12 N/m²;

1. Width a and height b of each bar cross - section ( Fig.12)

= 4.01 mm

= 4.5 mm

2. Flexible element stiffness

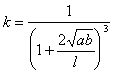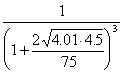== 0.724

= 1.2x10⁴ N/mm

3. Maximal alterating stress at maximal damper displacement d=0.275 ii

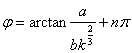== 47ⁱ48’

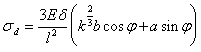= == 151 MPa

4 . Weight displacement

d₀ = G/K = 1700/1.2x10⁴ = 0.14 mm

So the flexible bushing may be preliminary displaced 0.14mm upwards as to be centered under the weight load. Then the d=0.275mm clearance will be uniform in circumferential direction.

5 Static stress in bars under the weight load

= 152(0.14/0.275) = 77.5 MPa